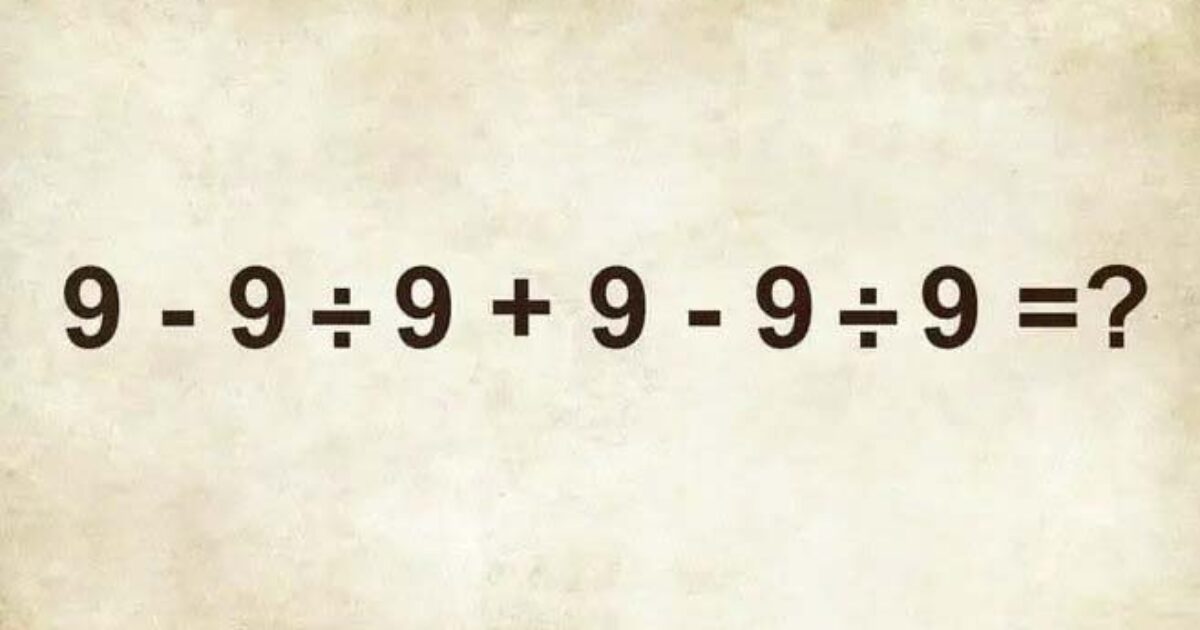Défi mathématique à résoudre : Un casse-tête pour les esprits curieux

Découvrez les mystères des problèmes mathématiques en apparence simples, mais qui cachent des défis insoupçonnés. Plongez dans les subtilités des priorités des opérations pour tester vos compétences !
La confusion des priorités : pourquoi tant de personnes commettent des erreurs ?
Combien de fois avons-nous été témoins de calculs simples semant la confusion, même parmi les amateurs de mathématiques ? Reprenons l’exemple : 48 ÷ 8(14 – 8). Souvent, les règles de priorité des opérations sont mal interprétées. Pourquoi ? Parce que la multiplication implicite, symbolisée par la juxtaposition (comme dans 8(6)), n’est pas toujours évidente.
Voici ce qu’il est important de retenir :
- Les parenthèses ne se limitent pas à leur contenu : elles englobent également tout facteur directement lié à elles.
- La multiplication par juxtaposition a une priorité plus élevée que la division ordinaire.
L’approche détaillée : la méthode correcte
Pour résoudre de manière précise l’équation 48 ÷ 8(14 – 8), il est essentiel de respecter l’ordre des opérations (PEMDAS ou BODMAS). Voici les étapes à suivre :
-
Calculer ce qui se trouve à l’intérieur des parenthèses :
14 − 8 = 6.
L’équation se transforme alors en : 48 ÷ 8(6).
-
Appliquer la multiplication implicite :
Ici, 8(6) est équivalent à 8 × 6 = 48.
Ainsi, l’équation devient : 48 ÷ 48.
-
Effectuer la division :
48 ÷ 48 = 1.
Résultat final : 1.
Pourquoi l’autre méthode est-elle erronée ?
De nombreuses personnes interprètent l’équation de la manière suivante :
-
Résolution des parenthèses :
14 − 8 = 6, ce qui conduit à 48 ÷ 8 × 6.
-
Division et multiplication de gauche à droite :
48 ÷ 8 = 6, suivi de 6 × 6 = 36.
Cette méthode peut sembler correcte mais néglige un point crucial :
La multiplication par juxtaposition (8(6)) est prioritaire. L’ignorer revient à enfreindre les règles de priorité des opérations.
Se souvenir des points essentiels : éviter les erreurs

Lorsque vous rencontrez un nombre accolé à des parenthèses (ex. 8(6)), considérez cela comme une entité unique.
Respectez toujours l’ordre des priorités : Parenthèses > Multiplication implicite > Division.
En conclusion, ce défi va au-delà d’un simple exercice mathématique. Il met en évidence l’importance de comprendre les subtilités des mathématiques pour éviter les erreurs face à des équations en apparence simples.