Ce célèbre casse-tête triangulaire résiste à votre perspicacité
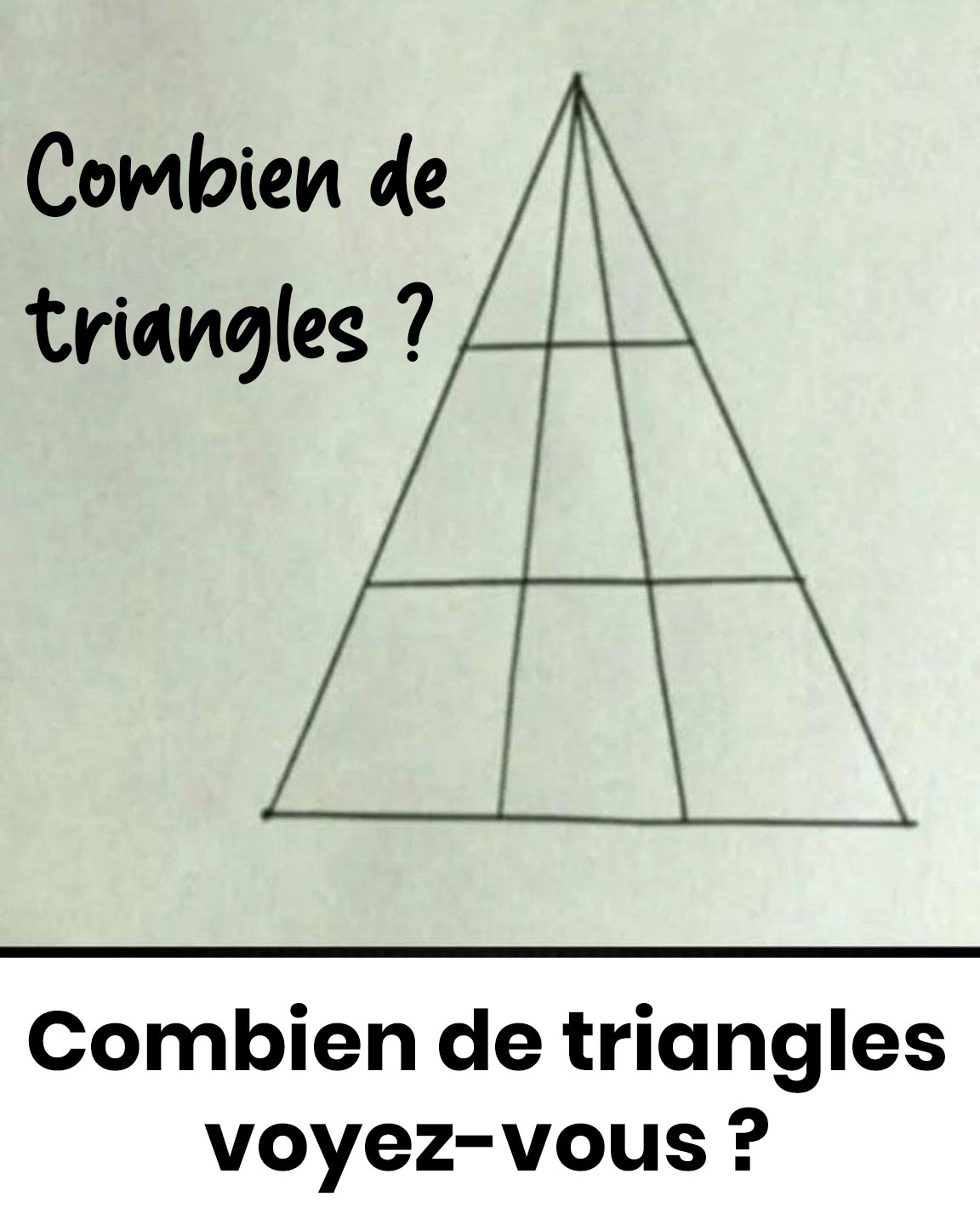
Ce qui semble être une simple figure géométrique dissimule en réalité une complexité insoupçonnée. Préparez-vous à découvrir pourquoi la majorité des observateurs passent à côté de la solution exacte dans cette énigme visuelle déconcertante.
L’illusion des triangles invisibles
Notre perception visuelle a tendance à capturer les formes triangulaires les plus apparentes tout en négligeant celles qui se créent par l’assemblage de plusieurs sections. Conséquence : nous tombons systématiquement dans la sous-estimation. Dans cette disposition classique (4 niveaux créés par 3 lignes parallèles au côté inférieur), le nombre correct s’élève à 27.
Si vous aviez obtenu 26, vous avez vraisemblablement omis un grand triangle composite — généralement une forme orientée vers le haut s’étendant sur 3 étages, ou une configuration partielle sur un côté.
Technique progressive : dénombrer avec précision

Identifiez les triangles « pointant vers le haut » en fonction de leur dimension verticale :
- Dimension 1 niveau : 10
- Dimension 2 niveaux : 6
- Dimension 3 niveaux : 3
- Dimension 4 niveaux : 1
Sous-total « orientés vers le haut » : 10 + 6 + 3 + 1 = 20.
Incorporez les triangles « dirigés vers le bas » générés par l’entrelacement des segments : 7.
Résultat final : 20 + 7 = 27.
Astuce mémorielle : retenez « 20 pour les supérieurs + 7 pour les inférieurs » et vous échapperez à l’erreur habituelle.
L’équation mathématique démystifiée

Vous souhaitez une méthode accélérée ? Pour une figure triangulaire principale segmentée en n rangées via des tracés parallèles à la base (ici n = 4), cette équation s’applique :
T(n) = n × (n + 2) × (2n + 1) ÷ 8
Avec n = 4 :
T = 4 × 6 × 9 ÷ 8 = 27
Ce chiffre concorde parfaitement avec notre calcul manuel. L’élégance de cette formule réside dans sa capacité à intégrer automatiquement toutes les configurations dimensionnelles, y compris les combinaisons multi-niveaux. Parfait pour valider son raisonnement… ou remporter une discussion passionnée !
Pièges récurrents (et comment s’en préserver)
- Dénombrer « par étages » sans considérer les grandes formes transversales : l’oubli caractéristique concerne souvent un triangle de 3 niveaux.
- Négliger les triangles inversés (« vers le bas ») : moins évidents visuellement, mais parfaitement existants (7 au total).
- Imaginer des lignes verticales supplémentaires : certaines versions incluent effectivement des verticales, ce qui influence le résultat (mais jamais vers 26). Vérifiez toujours la structure précise avant de statuer.
- Compter deux fois certaines formes : adoptez une progression méthodique par taille pour prévenir les répétitions.
Vous voulez approfondir ?
- Modifiez le nombre de niveaux : expérimentez la formule avec n = 3 ou n = 5 et confrontez avec un décompte visuel — excellent pour aiguiser votre perception.
- Jouez contre la montre : accordez-vous 60 secondes pour parvenir à 27. La clé ? Dénombrez d’abord les « supérieurs », puis ajoutez les « inférieurs ».
- Transmettez l’astuce : expliquer une méthode, c’est l’ancrer durablement dans votre mémoire (et assurer votre victoire lors des prochains défis intellectuels).
Car derrière une apparence géométrique élémentaire se niche souvent une leçon de logique appliquée… et la satisfaction subtile de conclure en maître !









